单源最短路径

1. 简介#

单源最短路径问题是图论中的一个非常经典的问题，它的目标是在一个带权的有向图或无向图中，找到从一个指定的“源”顶点到图中所有其他顶点的最短路径（路径上所有边的权重之和最小）。这个问题在实际生活中有很多重要的应用，比如网络路由、地图导航、通信网络优化等。

主要的单源最短路径算法主要有以下三个：

Dijkstra 算法：最著名和最常用的算法，但前提是图中所有边的权重都必须是非负的。
Bellman-Ford 算法：比 Dijkstra 算法更具普适性，可以处理带有负权重边的图。同时，它还能检测图中是否存在“负权环”。
SPFA 算法 (Shortest Path Faster Algorithm)：这是 Bellman-Ford 算法的一种优化版本，在很多情况下（特别是稀疏图）比 Bellman-Ford 更快，同样可以处理负权边和检测负权环。

2. Dijkstra 算法#

Dijkstra 算法（迪杰斯特拉算法） 是一种贪心算法。它的核心思想是，每次都从“尚未确定最短路径”的顶点中，选择一个距离源点最近的顶点，并且认为这个顶点的最短路径已经确定，然后用这个顶点去更新其他相邻顶点的距离。

算法步骤如下：

初始化：
- 创建一个距离数组 dist，dist[i] 表示从源点 startNode 到顶点 i 的当前最短距离。将 dist[startNode] 初始化为 0，其他所有顶点的 dist 初始化为无穷大 (INF)。
- 创建一个优先队列 pq，并将 {0, startNode}（表示距离为0，顶点为 startNode）加入队列。优先队列会根据距离从小到大排序。
主循环：当优先队列不为空时，执行以下操作：
- 从优先队列中取出距离最小的顶点 u（以及其距离 d）。
- 如果 d 大于 dist[u]，说明已经有更短的路径到达 u 了（这个旧的、较长的路径信息是冗余的），直接跳过本次循环。
- 遍历 u 的所有邻接点 v（权重为 w），进行松弛操作：如果通过 u 到达 v 的路径比已知的到 v 的最短路径还要短（即 dist[u] + w < dist[v]），那么就更新 dist[v] 为 dist[u] + w，并将新的、更短的路径信息 {dist[v], v} 加入优先队列。
结束：循环结束后，dist 数组中就存储了从源点到所有其他顶点的最短路径长度。

C++ 代码实现如下：

#include <iostream>
#include <vector>
#include <queue>
#include <limits>

const int INF = std::numeric_limits<int>::max(); // 代表无穷大

struct Edge
{
    int u, v, weight; // 边的起点、终点和权重
};

//{权重，顶点}
using ipair = std::pair<int, int>; // 用于存储权重和顶点的对

// Dijkstra 算法实现
// V: 顶点数量
// startNode: 源点
// Edge: 图的边列表{u, v, weight}
void dijkstra(int V, int startNode, std::vector<Edge> edges)
{
    // 距离数组，初始化为无穷大
    std::vector<int> dist(V, INF);
    dist[startNode] = 0;

    // 邻接表表示图
    std::vector<std::vector<ipair>> adj(V);
    for (const auto &edge : edges)
    {
        // 有向图
        adj[edge.u].push_back({edge.weight, edge.v});
        // 如果是无向图，则添加以下行
        // adj[edge.v].push_back({edge.weight, edge.u});
    }

    // 优先队列（最小堆），存储 {距离, 顶点}
    // std::greater 使其成为最小堆
    std::priority_queue<ipair, std::vector<ipair>, std::greater<ipair>> pq;

    pq.push({0, startNode});

    while (!pq.empty())
    {
        // 取出当前已知最短路径的顶点
        int u = pq.top().second;
        int d = pq.top().first;
        pq.pop();

        // 如果这个顶点的最短路径已经被更新过，则跳过
        if (d > dist[u])
        {
            continue;
        }

        // 遍历所有邻接点
        for (auto &edge : adj[u])
        {
            int v = edge.second;
            int weight = edge.first;

            // 松弛操作
            if (dist[u] + weight < dist[v])
            {
                dist[v] = dist[u] + weight;
                pq.push({dist[v], v});
            }
        }
    }

    // 打印从源点到所有顶点的最短距离
    std::cout << "Dijkstra 算法的结果：" << std::endl;
    for (int i = 0; i < V; ++i)
    {
        if (dist[i] == INF)
        {
            std::cout << "顶点 " << startNode << " -> " << i << ": No path" << std::endl;
        }
        else
        {
            std::cout << "顶点 " << startNode << " -> " << i << ": " << dist[i] << std::endl;
        }
    }
}

int main()
{
    int V = 7; // 顶点数
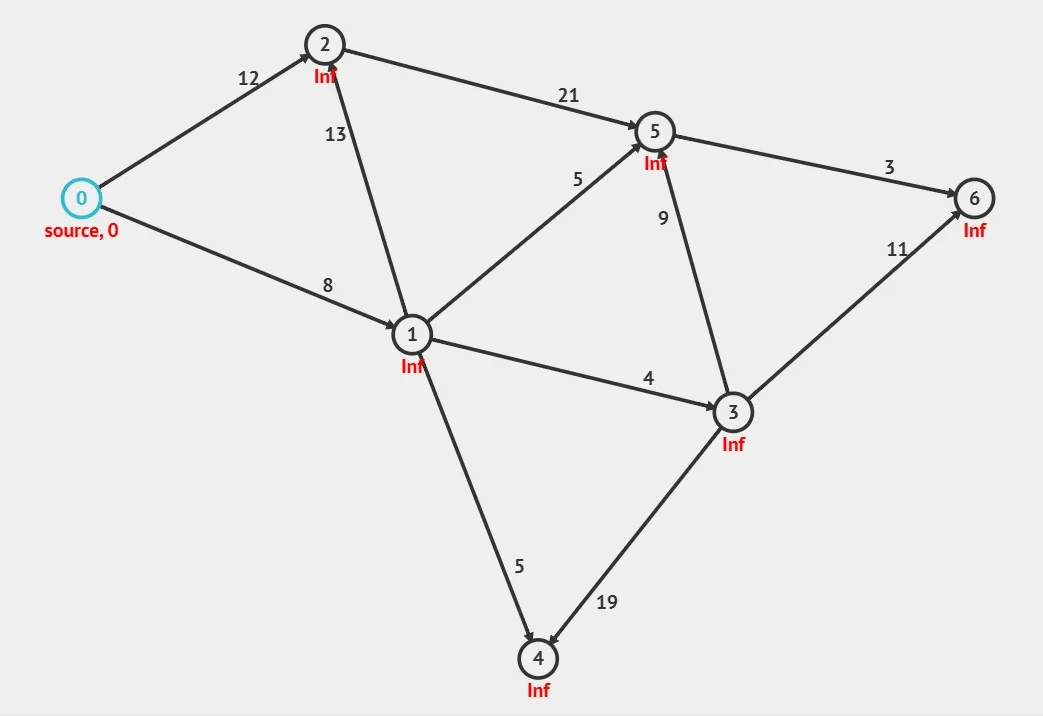
    int startNode = 0;

    std::vector<Edge> edges =
        {
            {0, 1, 8},
            {0, 2, 12},
            {0, 3, 19},
            {0, 4, 21},
            {1, 2, 13},
            {1, 3, 4},
            {1, 4, 5},
            {1, 5, 5},
            {2, 5, 21},
            {3, 4, 19},
            {3, 6, 11},
            {5, 3, 9},
            {5, 6, 3}};

    dijkstra(V, startNode, edges);
    return 0;
}

cpp

代码输出：

Dijkstra 算法的结果：
顶点 0 -> 0: 0
顶点 0 -> 1: 8
顶点 0 -> 2: 12
顶点 0 -> 3: 12
顶点 0 -> 4: 13
顶点 0 -> 5: 13
顶点 0 -> 6: 16

plaintext

动画演示过程如下：

alt text

3. Bellman-Ford 算法#

Bellman-Ford 算法（贝尔曼-福特算法） 同样用于解决单源最短路径问题，但它比 Dijkstra 更强大，因为它可以处理带负权边的图，并且能够检测负权环。

Bellman-Ford 的核心思想是动态规划。它通过对图中所有的边进行 V-1 轮松弛操作来逐步逼近最短路径。

经过第 1 轮松弛，可以找到从源点出发、最多经过 1 条边的最短路径。
经过第 2 轮松弛，可以找到从源点出发、最多经过 2 条边的最短路径。
经过 V-1 轮松弛，可以找到从源点出发、最多经过 V-1 条边的最短路径。因为在一个不包含负权环的图中，任意两点间的最短路径最多包含 V-1 条边。

算法步骤如下：

初始化：
- 创建一个距离数组 dist，将源点 startNode 的距离 dist[startNode] 初始化为 0，其他所有顶点的 dist 初始化为无穷大 (INF)。
迭代松弛：
- 重复 V-1 次以下操作：
- 遍历图中的每一条边 (u, v)，其权重为 w。
- 松弛操作：如果 dist[u] + w < dist[v]，则更新 dist[v] 为 dist[u] + w。
检测负权环：
- 完成 V-1 轮松弛后，再进行第 V 轮松弛：
- 遍历图中的每一条边 (u, v)。
- 如果仍然可以进行松弛操作（即 dist[u] + w < dist[v]），则说明图中存在一个从源点可达的负权环。因为在没有负权环的情况下，V-1 轮后所有最短路径都已确定，不应再有更新。

C++ 代码实现如下：

#include <iostream>
#include <vector>
#include <queue>
#include <limits>

const int INF = std::numeric_limits<int>::max(); // 代表无穷大

struct Edge
{
    int u, v, w; // 边的起点、终点和权重
};

// Bellman-Ford 算法实现
// V: 顶点数量, E: 边的数量
// edges: 边的列表
// startNode: 源点
void bellmanFord(int V, int startNode, const std::vector<Edge> &edges)
{
    std::vector<int> dist(V, INF);
    dist[startNode] = 0;

    // 1. 进行 V-1 轮松弛操作
    for (int i = 0; i < V - 1; ++i)
    {
        for (const auto &edge : edges)
        {
            if (dist[edge.u] != INF && dist[edge.u] + edge.w < dist[edge.v])
            {
                dist[edge.v] = dist[edge.u] + edge.w;
            }
        }
    }

    // 2. 检测负权环
    bool hasNegativeCycle = false;
    for (const auto &edge : edges)
    {
        if (dist[edge.u] != INF && dist[edge.u] + edge.w < dist[edge.v])
        {
            hasNegativeCycle = true;
            break;
        }
    }

    // 3. 打印结果
    std::cout << "Bellman-Ford 算法的结果：" << std::endl;
    if (hasNegativeCycle)
    {
        std::cout << "图中包含负权重环！" << std::endl;
    }
    else
    {
        for (int i = 0; i < V; ++i)
        {
            if (dist[i] == INF)
            {
                std::cout << "顶点 " << startNode << " -> " << i << ": No path" << std::endl;
            }
            else
            {
                std::cout << "顶点 " << startNode << " -> " << i << ": " << dist[i] << std::endl;
            }
        }
    }
}
int main()
{
    int V = 6; // 顶点数
    int startNode = 0;

    std::vector<Edge> edges =
        {
            {0, 1, -5},
            {0, 2, 2},
            {1, 2, 3},
            {1, 3, 4},
            {1, 4, 5},
            {2, 5, 1},
            {3, 4, 2},
            {3, 5, 2},
            {4, 5, 3},
            {5, 1, -2}};

    bellmanFord(V, startNode, edges);
    return 0;
}

cpp

代码输出：

Bellman-Ford 算法的结果：
顶点 0 -> 0: 0
顶点 0 -> 1: -5
顶点 0 -> 2: -2
顶点 0 -> 3: -1
顶点 0 -> 4: 0
顶点 0 -> 5: -1

plaintext

4. SPFA 算法#

SPFA 算法是 Bellman-Ford 算法的一种队列优化版本，同样用于解决单源最短路径问题，并且能够处理负权边和检测负权环。

Bellman-Ford 算法的瓶颈在于它每一轮迭代都会盲目地尝试松弛所有的边，而实际上，只有那些在上一轮中距离被缩短了的顶点，才有可能去更新它们的邻接点。而SPFA 算法正是基于这个观察进行优化。它维护一个队列，队列中存放的是“刚刚被成功松弛过”的顶点。算法每次从队列中取出一个顶点 u，然后用 u 去松弛它的所有邻接点 v。如果 v 被成功松弛，并且 v 当前不在队列中，就将 v 加入队列。这个过程不断重复，直到队列为空。

由于只有“可能引发更新”的顶点才会入队并被用于松弛操作，SPFA 在大多数情况下（尤其是稀疏图）避免了 Bellman-Ford 中的大量冗余计算，因此平均效率要高得多。

算法步骤如下：

初始化：
- 创建一个距离数组 dist，将源点 startNode 的距离 dist[startNode] 初始化为 0，其他所有顶点的 dist 初始化为无穷大 (INF)。
- 创建一个队列 q，并将源点 startNode 入队。
- 创建一个布尔数组 in_queue，用于标记顶点是否在队列中。将 in_queue[startNode] 设为 true。
- 创建一个计数器数组 count，count[i] 记录顶点 i 入队的次数，用于检测负权环。
主循环：当队列 q 不为空时：
- 从队首取出一个顶点 u，并将其出队。将 in_queue[u] 设为 false。
- 遍历 u 的所有邻接点 v（权重为 w）：
  - 松弛操作：如果 dist[u] + w < dist[v]，则更新 dist[v] 为 dist[u] + w。
  - 如果 v 被成功松弛，且 v 当前不在队列中：
  - 将 v 入队，并设置 in_queue[v] 为 true。
  - 增加 v 的入队计数 count[v]。
  - 检测负权环：如果 count[v] 大于等于图的顶点总数 V，则说明从源点到 v 的路径上存在一个负权环。算法可以立即终止并报告。
结束：如果队列为空且没有检测到负权环，dist 数组就包含了源点到所有其他顶点的最短路径。

C++ 代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <limits>

const int INF = std::numeric_limits<int>::max(); // 代表无穷大

struct Edge
{
    int to;     // 边的终点
    int weight; // 边的权重
};

// SPFA 算法实现
// V: 顶点数量
// adj: 邻接表表示的图
// startNode: 源点
void spfa(int V, int startNode, const std::vector<std::vector<Edge>> &adj)
{
    std::vector<int> dist(V, INF);
    std::vector<int> inQueueCount(V, 0); // 记录每个顶点入队的次数
    std::vector<bool> inQueue(V, false); // 标记顶点是否在队列中
    std::queue<int> q;

    dist[startNode] = 0;
    q.push(startNode);
    inQueue[startNode] = true;
    inQueueCount[startNode]++;

    bool hasNegativeCycle = false;

    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        inQueue[u] = false;

        for (const auto &edge : adj[u])
        {
            int v = edge.to;
            int w = edge.weight;

            if (dist[u] != INF && dist[u] + w < dist[v])
            {
                dist[v] = dist[u] + w;
                if (!inQueue[v])
                {
                    q.push(v);
                    inQueue[v] = true;
                    inQueueCount[v]++;
                    // 如果一个顶点入队次数超过 V，则存在负权环
                    if (inQueueCount[v] > V)
                    {
                        hasNegativeCycle = true;
                        goto end_loop; // 跳出外层循环
                    }
                }
            }
        }
    }

end_loop:;

    // 3. 打印结果
    std::cout << "SPFA 算法的结果：" << std::endl;
    if (hasNegativeCycle)
    {
        std::cout << "图中包含负权重环！" << std::endl;
    }
    else
    {
        for (int i = 0; i < V; ++i)
        {
            if (dist[i] == INF)
            {
                std::cout << "顶点 " << startNode << " -> " << i << ": No path" << std::endl;
            }
            else
            {
                std::cout << "顶点 " << startNode << " -> " << i << ": " << dist[i] << std::endl;
            }
        }
    }
}

int main()
{
    int V = 6; // 顶点数
    int startNode = 0;

    // 为了使用 SPFA，最好将边列表转换为邻接表
    std::vector<std::vector<Edge>> adj(V);
    std::vector<std::pair<int, std::pair<int, int>>> edges =
        {
            {0, {1, -5}},
            {0, {2, 2}},
            {1, {2, 3}},
            {1, {3, 4}},
            {1, {4, 5}},
            {2, {5, 1}},
            {3, {4, 2}},
            {3, {5, 2}},
            {4, {5, 3}},
            {5, {1, -2}}};

    for (const auto &edge_info : edges)
    {
        int u = edge_info.first;
        int v = edge_info.second.first;
        int w = edge_info.second.second;
        adj[u].push_back({v, w});
    }

    spfa(V, startNode, adj);
    return 0;
}

cpp

输出结果为：

SPFA 算法的结果：
顶点 0 -> 0: 0
顶点 0 -> 1: -5
顶点 0 -> 2: -2
顶点 0 -> 3: -1
顶点 0 -> 4: 0
顶点 0 -> 5: -1

cpp