进位计数制及数制之间的互转

1.前言#

本文主要介绍进位计数制和数制之间的相互转换。

2. 进位计数制#

按照进位的方法进行计数，称为进位计数制。在进位制中每个数规定使用的数码符号的数量，称为进位基数，例如十进制的进位基数是10，二进制的进位基数是2。使用 $R$ 为基数的计数制称为 $R$ 进制数，常用的有十进制数、二进制数、十六进制数和八进制数。

我们习惯把最右边一位称为最低位，最左边一位称为最高位。权值是进位基数从右至左呈指数规律增加，最低位权值位 $R^0$ ，第 $i$ 位的权值为 $R^i$ 。这样就可以把 $R$ 进制中数 $N$ 写成按权展开的多项式：

N_R = a_{n-1}R^{n-1} + \cdots + a_iR^i + \cdots + a_0R^0 + a_{-1}R^{-1} + a_{-2}R^{-2} + \cdots + a_{-m}R^{-m}

2.1 十进制数(Decimal)#

十进制是我们非常熟悉的数制，它的进位基数是10。各位的权值就是我们通常所说的“个”、“十”、“百”、“千”、“万”等。以520.1314为例：

数码	5	2	0	1	3	1	4
权值	$10^2$	$10^1$	$10^0$	$10^{-1}$	$10^{-2}$	$10^{-3}$	$10^{-4}$
总计	500	20	0	0.1	0.03	0.001	0.0004

2.2 二进制数(Binary)#

计算机采用的是“0”和“1”两个基本符号组成的二进制码，因为计算机内部记忆信息的设备由两个状态的器件组成，因而计算机内部的任何信息只能用“0”或“1”这两个状态来表示。17世纪至18世纪的德国数学家莱布尼茨，是世界上第一个提出二进制记数法的人。

二进制的基数为2，逢2进1。以0101.1110为例：

数码	0	1	0	1	1	1	1	0
权值	$2^{3}$	$2^{2}$	$2^{1}$	$2^{0}$	$2^{-1}$	$2^{-2}$	$2^{-3}$	$2^{-4}$
总计	0	4	0	1	0.5	0.25	0.125	0

所以该数表示的是10进制中的：0+4+0+1+0.5+0.25+0.125+0=5.875

同时，二进制的运算具有如下法则：

加法
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0, 向下一位进1
乘法
- 0×0=0
- 1×0=0
- 0×1=0
- 1×1=1
减法
- 0 - 0=0
- 1 - 0=1
- 1 - 1=0，
- 0 - 1=1，向前一位借1
除法（除数只能为1）
- 0÷1=0
- 1÷1=1

2.3 十六进制(Hexadecimal)#

十六进制的基数为16，是一种逢16进1的进位制。通常用数字0、1、2、3、4、5、6、7、8、9和字母A、B、C、D、E、F（a、b、c、d、e、f）表示，其中:A ~ F表示10 ~ 15。以58C.B2为例：

数码	5	8	C	B	2
权值	$16^2$	$16^1$	$16^0$	$16^{-1}$	$16^{-2}$
总计	1280	128	12	0.6875	0.0078125

所以该数表示的是十进制中的：1280+128+12+0.6875+0.0078125=1420.6953125

2.4 八进制(Octal)#

八进制的基数为8，采用0，1，2，3，4，5，6，7八个数字，逢八进1。以520.1为例：

数码	5	2	0	1
权值	$8^2$	$8^1$	$8^0$	$8^{-1}$
总计	320	16	0	0.125

所以该数表示的是10进制中的：320+16+0+0.125=336.125

3. 数制间的转换#

其实上面在介绍数制时，我们已经可以窥见它们之间的转换关系，下面进一步明确和总结。

3.1 非十进制数转换为十进制数#

这一过程非常简单，由上面的介绍我们可以知道如下的关系式：

a_n R^n + a_{n-1} R^{n-1} + \cdots + a_i R^i + \cdots + a_0 = d_m 10^m + d_{m-1} 10^{m-1} + \cdots + d_i 10^i + \cdots + d_1 10 + d_0

我们只需要将 $R^i$ 和 $a^i$ 用十进制表示，然后作十进制运算即可。这样描述可能比较难以理解，我们举个例子：

(1011.101)_2 = 1 \times 2^3 + 1 \times 2^1 + 1 \times 2^0 + 1 \times 2^{-1} + 1 \times 2^{-3} = (11.625)_{10}

其他进制也同理：

(3B6)_{16} = 3 \times 16^2 + 11 \times 16^1 + 6 = 768 + 176 + 6 = (950)_{10}

3.2 十进制数转换为非十进制数#

最常用的方法是“除R取余法”：即只需将要被转换的十进制数，连续除以R，直至商等于零为止。第一次除法的余数是 $a_0$ ，而最后一次除法的余数为 $a_n$ ，将 $a_n$ ~ $a_1$ 从高到低排列得 $a_n...a_1$ ，即为所求R进制数。

将 $(251)_{10}$ 转换为二进制数的过程如下：

结果为： $(11111011)_2$

将 $(251)_{10}$ 转换为十六进制数的过程如下：

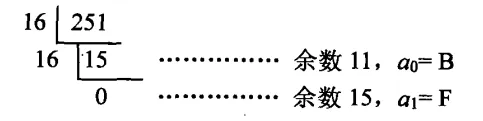
结果为： $(FB)_{16}$

把十进制小数转换为相应R进制小数时，可以采用“乘R取整法”：即对该小数或乘以基数R后所得的新的小数部分进行乘以基数R的操作，所得整数为R进制的小数位，第一次乘法的余数是 $K_{-1}$ ，而最后一次乘法的余数为 $K_{-n}$ ，将 $K_{-1}$ ~ $K_{-n}$ ，从高到低排列得 $K_{-1}…K_{-n}$ ，即为所求R进制小数。

将 $(0.6875)_{10}$ 转换为二进制数过程如下：

结果为： $(0.1011)_2$

将 $(0.6875)_{10}$ 转换为十六进制数过程如下：

结果为： $(0.BH)_{16}$

并不是所有的小数都能在不同的进制中进行转换，因为不同进制的精度是不一样的，有时候会出现除不尽的情况。

将 $(0.734)_{10}$ 转换为二进制数过程如下：

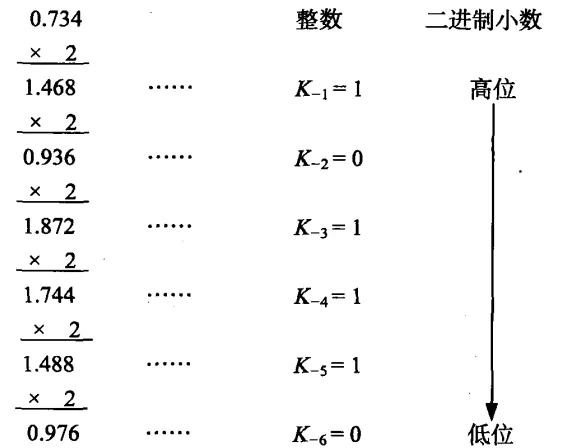
结果为： $(0.101110)_2$ （无穷小数）

综上，如果任意一个十进制数要转换为非十进制数，可以把整数部分和小数部分分别加以转换，然后把转换后的整数部分和小数部分相加即可。

上述的办法不是唯一的转换方法，上述方法非常利于人类进行计算，因为它只涉及除以2，但是这种方法对于机器来说是不理想的。首先这种方法运用的是除法，机器在进行除法运算的时候是非常耗时的；其次机器需要存储计算出的比特，以便稍后以相反的顺序打印。下面以将 $(148)_{10}$ 转换为二进制数为例，说明另一种方法：

首先从小于148的2的最大次幂——128开始比较
148 $\ge$ 128，因此该位为1，148-128=20
20<64，因此该位为0，20
20<32，因此该位为0，20
20 $\ge$ 16，因此该位为1，20-16=4
4<8，因此该位为0，4
4 $\ge$ 4，因此该位为1，4-4=0
0<2，因此该位为0，0
0<1，因此该位为0，0

所以最后的结果为：10010100

如果含有小数部分，也可以仿照该方法进行逐级比较。

这种方法对于人类来说在小数字时（例如 8 位二进制数）相当简单。对于机器来说也很高效，因为每个位只需要需要比较、减法和赋值。

当数字较小，我们手动计算进行转换时，两种方法都可。如果数字较大，我们进行手动计算时选用第一种方法，编写代码时选用第二种方法。

3.3 二进制转换为八进制、十六进制#

二进制转换为八进制、十六进制的方法为分组转换。如果转换为八进制，则从左开始，三位一组，不足补零；如果转换为十六进制，则从右开始，四位一组，不足补零。下面以将 $(10110110)_2$ 转换为八进制和十六进制为例。

转换为八进制：
$(\underline{010}\:\underline{110}\:\underline{110})_2$ $(\underline{2}\:\underline{6}\:\underline{6})_{8}$
转换为十六进制：
$(\underline{1011}\:\underline{0110})_2$ $(\underline{B}\:\underline{6})_{16}$

3.4 八进制、十六进制转换为二进制#

八进制、十六进制转换为二进制的方法也非常简单。如果是八进制转换为二进制，只需要将八进制的每一位用3位的二进制表示即可；如果是十六进制转换位二进制，只需要将十六进制的每一位用4位的二进制表示即可。

将 $(57)_{8}$ 转换为二进制：

(\underline{5}\:\underline{7})_8

(\underline{101}\:\underline{111})_2

将 $(A9)$ 转换为二进制：

(\underline{A}\:\underline{9})_{16}

(\underline{1011}\:\underline{1010})_{2}

3.5 八进制和十六进制的相互转换#

八进制和十六进制的相互转换可以通过二进制为中介进行转换。非常简单，这里不再举例。

4. 参考资料#

《微机原理、汇编语言与接口技术》人民邮电出版社
O.4 — Converting integers between binary and decimal representation – Learn C++ ↗