liangbm3's blog

Back
15 min read

二叉树的遍历小结

总结一下二叉树的遍历
views | comments

1. 二叉树的遍历方式#

二叉树的遍历方式可以分为深度遍历和广度遍历两种。

所谓的深度遍历，就是深度优先的原则，先把一条路径走到头再回头，对于二叉树就是选择一条路径走到叶子节点之后再考虑其他路径。二叉树的深度遍历又可以分为前序遍历、中序遍历、后序遍历三种，这三种遍历方式的访问顺序分别为：

  • 前序遍历：根节点->左子树->右子树
  • 中序遍历：左子树->根节点->右子树
  • 后序遍历：左子树->右子树->根节点

而所谓的广度遍历，就是广度优先的原则。对于二叉树来说，就是一层一层地访问，所以又叫层序遍历。

以下面这个二叉树为例：

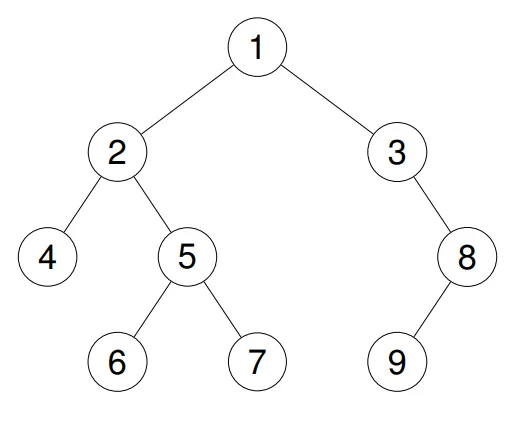
alt text

  • 前序遍历：1->2->4->5->6->7->3->8->9
  • 中序遍历：4->2->6->5->7->1->3->9->8
  • 后序遍历：4->6->7->5->2->9->8->3->1
  • 层序遍历：1->2->3->4->5->8->6->7->9

2. 二叉树遍历的代码实现#

在遍历之前，先定义节点，以及构建上面示例的二叉树。

节点定义：

//节点定义
struct TreeNode
{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int val):val(val),left(nullptr),right(nullptr){}
};
cpp

构建二叉树：

TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->right = new TreeNode(8);
root->left->right->left=new TreeNode(6);
root->left->right->right=new TreeNode(7);
root->right->right->left=new TreeNode(9);
cpp

2.1 前序遍历#

先来看递归版本：

//前序遍历递归版本
void preorder_recursion(TreeNode* root)
{
    if(root==nullptr)
    {
        return ;
    }
    cout<<root->val<<" ";
    preorder_recursion(root->left);
    preorder_recursion(root->right);
}
cpp

因为深度优先的的原则通常是用递归来实现的，因此递归的代码非常简单。当到达某个节点时，我们将它的val值打印出来，即记录该节点的值。根据前序遍历的定义，我们先访问根节点的值，然后访问左子树，再访问右子树。所以在递归访问左子树之前，就需要记录根节点的值。

现在来看迭代版本，所谓的迭代版本，就是不借助递归调用函数来实现，递归的时候隐式地维护了一个栈，迭代版本就是显式地把这个栈模拟出来。前序遍历的迭代版本如下：

//前序遍历迭代版本
void preorder_iteration(TreeNode* root)
{
    stack<TreeNode*> st;
    while(!st.empty()||root!=nullptr)
    {
        while(root!=nullptr)
        {
            cout<<root->val<<" ";//记录根节点的值
            //将根节点入栈，这里入栈是为了访问完左子树之后，能够根据根节点去访问右子树
            st.push(root);
            root=root->left;//访问左子树，
        }
        //左子树访问完之后，根节点出栈
        root=st.top();
        st.pop();
        root=root->right;//访问右子树
    }
}
cpp

2.1 中序遍历#

先来看递归版本：

//中序遍历递归版本
void inorder_recursion(TreeNode* root)
{
    if(root==nullptr)
    {
        return ;
    }
    inorder_recursion(root->left);
    cout<<root->val<<" ";
    inorder_recursion(root->right);
}
cpp

中序遍历的递归版本的代码和前序遍历非常相似，只是记录节点的位置不同。根据定义，先访问左子树，再访问根节点，最后再访问右子树，因此记录根节点的位置在中间。

中序遍历的迭代版本如下：

//中序遍历迭代版本
void inorder_iteration(TreeNode* root)
{
    stack<TreeNode*> st;
    while(!st.empty()||root!=nullptr)
    {
        while(root!=nullptr)
        {
            //根节点入栈，为了能够访问完左子树之后，能够访问根节点和右子树
            st.push(root);
            root=root->left;//访问左子树
        }
        root=st.top();
        st.pop();
        cout<<root->val<<" ";//记录根节点的值
        root=root->right;//访问右子树
    }
}
cpp

中序遍历和前序遍历的迭代版本也非常相似，只是记录根节点的顺序不同。根据定义，中序遍历先访问左子树再访问根节点，因此记录根节点的位置放在了出栈的时候而不是入栈的时候。

其实这可以结合递归版本来理解的。前序遍历的递归版本在调用递归函数访问左子树之前，已经记录了根节点的值，而调用递归函数恰恰是入栈的过程。而中序遍历的递归版本在调用递归函数访问左子树之后，再记录根节点的值，即出栈之后。

2.3 后序遍历#

先来看递归版本：

//后序遍历递归版本
void postorder_recursion(TreeNode* root)
{
    if(root==nullptr)
    {
        return ;
    }
    postorder_recursion(root->left);
    postorder_recursion(root->right);
    cout<<root->val<<" ";
}
cpp

递归版本非常好理解，递归访问完左子树和右子树之后，记录根节点的值。

迭代版本如下：

//后序遍历迭代版本
void postorder_iteration(TreeNode* root)
{
    stack<TreeNode*> st;
    TreeNode* prev=nullptr;
    while (!st.empty()||root!=nullptr)
    {
        while(root!=nullptr)//递归访问左子树
        {
            st.push(root);
            root=root->left;
        }
        //访问完左子树之后
        root=st.top();//根节点出栈
        st.pop();
        //判断右子树是否已经访问了，如果右子树为空或者右子树已经访问了
        //则记录根节点的值。
        if(root->right==nullptr||prev==root->right)
        {
            cout<<root->val<<" ";
            prev=root;
            //这里的置空是为了在下一次循环中从栈中获取节点进行处理
            //而不是继续处理当前节点，因为记录了当前节点之后，
            //说明左右子树的节点都已经被处理完了
            root=nullptr;
        }
        //否则访问右子树
        else
        {
            st.push(root);
            root=root->right;
        }
    }
    
}
cpp

后序遍历的迭代版本是所有的遍历中最难理解的。我们先从后序遍历的递归版本看起，递归版本先递归访问左子树，再递归访问右子树后，再记录根节点的值。 递归访问左子树在迭代中的实现：

while(root!=nullptr)
{
    st.push(root);
    root=root->left;
}
cpp

这部分代码就是实现了递归访问左子树。后序遍历为什么和前序遍历和中序遍历有这么大差别呢？主要原因是记录值的位置不同，前序遍历在递归访问左子树前记录根节点的值，中序遍历在递归访问左子树后记录根节点的值。而后序遍历，在递归访问完左子树后，再递归访问右子树和记录节点的值。

在递归代码中，“再递归访问右子树和记录节点的值” 这个是很容易实现的，而在迭代版本中，递归的返回即是根节点的出栈，这时我们就需要判断右子树是否已经访问过了。如何判断呢？这里的方法是引入一个名为prev的辅助变量，记录上一次访问的节点。如果从栈弹出的节点的右孩子等于 prev 这个辅助变量， 说明访问的就是右子树，可以对当前节点进行记录了，否则需要访问右子树。

2.4 层序遍历#

层序遍历是广度优先的思想，广度优先遍历一般借助队列实现，代码如下：

//层序遍历
void levelorder(TreeNode* root)
{
    if(root==nullptr)
    {
        return;
    }
    queue<TreeNode*> q;
    q.push(root);
    while(!q.empty())
    {
        int sz=q.size();//获取当前层的节点个数
        for(int i=0;i<sz;i++)//对当前层进行遍历
        {
            TreeNode* node=q.front();
            q.pop();
            cout<<node->val<<" ";
            if(node->left) q.push(node->left);
            if(node->right) q.push(node->right);
        }
        cout<<endl;
    }
}
cpp

3. 代码汇总#

#include <iostream>
#include <vector>
#include <stack>
#include <queue>

using namespace std;

//节点定义
struct TreeNode
{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int val):val(val),left(nullptr),right(nullptr){}
};

//前序遍历递归版本
void preorder_recursion(TreeNode* root)
{
    if(root==nullptr)
    {
        return ;
    }
    cout<<root->val<<" ";
    preorder_recursion(root->left);
    preorder_recursion(root->right);
}

//前序遍历迭代版本
void preorder_iteration(TreeNode* root)
{
    stack<TreeNode*> st;
    while(!st.empty()||root!=nullptr)
    {
        while(root!=nullptr)
        {
            cout<<root->val<<" ";//记录根节点的值
            //将根节点入栈，这里入栈是为了访问完左子树之后，能够根据根节点去访问右子树
            st.push(root);
            root=root->left;//访问左子树，
        }
        //左子树访问完之后，根节点出栈
        root=st.top();
        st.pop();
        root=root->right;//访问右子树
    }
}

//中序遍历递归版本
void inorder_recursion(TreeNode* root)
{
    if(root==nullptr)
    {
        return ;
    }
    inorder_recursion(root->left);
    cout<<root->val<<" ";
    inorder_recursion(root->right);
}

//中序遍历迭代版本
void inorder_iteration(TreeNode* root)
{
    stack<TreeNode*> st;
    while(!st.empty()||root!=nullptr)
    {
        while(root!=nullptr)
        {
            //根节点入栈，为了能够访问完左子树之后，能够访问根节点和右子树
            st.push(root);
            root=root->left;//访问左子树
        }
        root=st.top();
        st.pop();
        cout<<root->val<<" ";//访问根节点
        root=root->right;//访问右子树
    }
}

//后序遍历递归版本
void postorder_recursion(TreeNode* root)
{
    if(root==nullptr)
    {
        return ;
    }
    postorder_recursion(root->left);
    postorder_recursion(root->right);
    cout<<root->val<<" ";
}

//后序遍历迭代版本
void postorder_iteration(TreeNode* root)
{
    stack<TreeNode*> st;
    TreeNode* prev=nullptr;
    while (!st.empty()||root!=nullptr)
    {
        while(root!=nullptr)//递归访问左子树
        {
            st.push(root);
            root=root->left;
        }
        //访问完左子树之后
        root=st.top();//根节点出栈
        st.pop();
        //判断右子树是否已经访问了，如果右子树为空或者右子树已经访问了
        //则记录根节点的值。
        if(root->right==nullptr||prev==root->right)
        {
            cout<<root->val<<" ";
            prev=root;
            //这里的置空是为了在下一次循环中从栈中获取节点进行处理
            //而不是继续处理当前节点，因为记录了当前节点之后，
            //说明左右子树的节点都已经被处理完了
            root=nullptr;
        }
        //否则访问右子树
        else
        {
            st.push(root);
            root=root->right;
        }
    }
    
}

//层序遍历
void levelorder(TreeNode* root)
{
    if(root==nullptr)
    {
        return;
    }
    queue<TreeNode*> q;
    q.push(root);
    while(!q.empty())
    {
        int sz=q.size();//获取当前层的节点个数
        for(int i=0;i<sz;i++)//对当前层进行遍历
        {
            TreeNode* node=q.front();
            q.pop();
            cout<<node->val<<" ";
            if(node->left) q.push(node->left);
            if(node->right) q.push(node->right);
        }
        cout<<endl;
    }
}

//删除二叉树
void deleteTree(TreeNode* node) {
    if (node == nullptr) return;
    
    deleteTree(node->left);
    deleteTree(node->right);
    
    delete node;
}

int main() {
    // 构建二叉树
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->right->right = new TreeNode(8);
    root->left->right->left=new TreeNode(6);
    root->left->right->right=new TreeNode(7);
    root->right->right->left=new TreeNode(9);

    cout<<"前序遍历递归版本："<<endl;
    preorder_recursion(root);
    cout<<endl;

    cout<<"前序遍历迭代版本："<<endl;
    preorder_iteration(root);
    cout<<endl;

    cout<<"中序遍历递归版本："<<endl;
    inorder_recursion(root);
    cout<<endl;

    cout<<"中序遍历迭代版本："<<endl;
    inorder_iteration(root);
    cout<<endl;

    cout<<"后序遍历递归版本："<<endl;
    postorder_recursion(root);
    cout<<endl;

    cout<<"后序遍历迭代版本："<<endl;
    postorder_iteration(root);
    cout<<endl;

    //层序遍历
    cout<<"层序遍历版本："<<endl;
    levelorder(root);
    cout<<endl;

    deleteTree(root);

    return 0;
}
cpp

输出结果：

前序遍历递归版本：
1 2 4 5 6 7 3 8 9 
前序遍历迭代版本：
1 2 4 5 6 7 3 8 9 
中序遍历递归版本：
4 2 6 5 7 1 3 9 8 
中序遍历迭代版本：
4 2 6 5 7 1 3 9 8 
后序遍历递归版本：
4 6 7 5 2 9 8 3 1 
后序遍历迭代版本：
4 6 7 5 2 9 8 3 1 
层序遍历版本：
1 
2 3 
4 5 8 
6 7 9
plaintext
二叉树的遍历小结
https://liangbm3.site/blog/er-cha-shu-de-bian-li-xiao-jie
Author liangbm3
Published at 2025年6月19日
Copyright CC BY-NC-SA 4.0

C++ 中的内存对齐

原码、补码和反码
Comment seems to stuck. Try to refresh?✨