拓扑排序 | liangbm3's blog

1. 拓扑排序简介#

拓扑排序是对 有向无环图 (Directed Acyclic Graph, DAG) 的顶点进行的一种线性排序。简单来说，就是将一个 DAG 中所有的顶点排成一个线性序列，使得图中任意一对顶点 u 和 v，若存在一条从 u 指向 v 的边 (u -> v)，那么在这个序列中 u 必须出现在 v 的前面。

拓扑排序主要用于解决依赖关系和执行顺序的问题，主要的应用场景如下：

任务调度或工作流：在一个复杂的项目中，很多任务之间有依赖关系。例如，编译代码时的文件依赖关系 (Makefile)。拓扑排序可以确定任务的执行顺序，确保依赖的任务先完成。
课程的先修关系。例如必须先修完《程序设计》才能修读《数据结构》，拓扑排序可以确定一个满足所有先修课要求的学习计划。
软件包的依赖管理。在安装或卸载软件包时，系统需要解决包之间的依赖关系，例如 Linux 的 apt-get 命令在安装一个包之前，会安装它的所有依赖包，这个依赖解析的过程就用到了拓扑排序。

2. 算法及实现#

实现拓扑排序有两种经典的算法：

Kahn 算法 (基于入度的算法)
基于深度优先搜索 (DFS) 的算法

以下面的这个有向无环图为例：

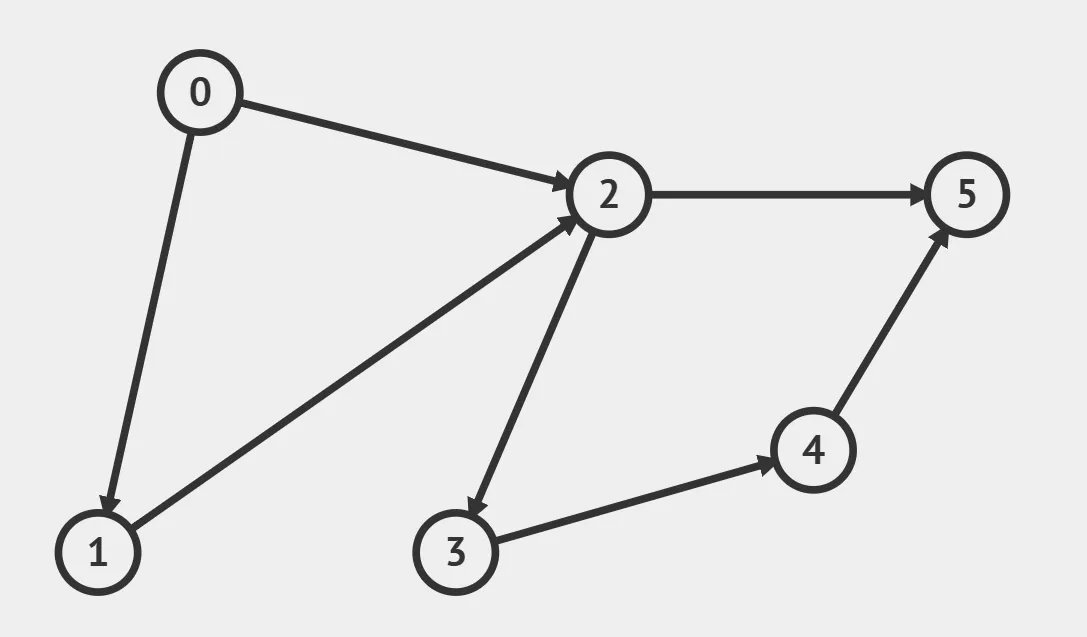
alt text

2.1 Kahn 算法#

Kahn 算法的思路非常直观，就像模拟 “完成任务” 的过程。一个任务只有在它所有的前置任务都完成后，才能开始执行。算法步骤如下：

计算所有顶点的入度。
- 入度是指有多少条边指向该顶点。
初始化一个队列，并将所有入度为 0 的顶点入队。
- 入度为 0 的顶点意味着它没有任何前置依赖，可以作为起点。
循环执行以下操作，直到队列为空：
- 从队列中取出一个顶点 u，并将其加入到最终的拓扑排序结果序列中。
- 遍历 u 的所有邻接顶点 v（即所有 u 指向的顶点）。
- 对于每一个邻接顶点 v，将其入度减 1 (相当于 u 这个前置任务已经完成了)。
- 如果 v 的入度变为 0，则将 v 入队。
检查结果：
- 如果最终结果序列中的顶点数量与图中顶点总数相等，则说明拓扑排序成功。
- 如果数量不相等，则说明图中存在环，无法进行拓扑排序。

Kahn 算法的 C++ 实现如下：

#include <iostream>
#include <vector>
#include <queue>
#include <string>

// Kahn 算法实现拓扑排序
std::vector<int> topologicalSort_Kahn(int n, const std::vector<std::vector<int>>& adj) 
{
    // 1. 计算所有顶点的入度
    std::vector<int> in_degree(n, 0);
    for (int i = 0; i < n; ++i) 
    {
        for (int neighbor : adj[i]) 
        {
            in_degree[neighbor]++;
        }
    }

    // 2. 将所有入度为 0 的顶点加入队列
    std::queue<int> q;
    for (int i = 0; i < n; ++i) 
    {
        if (in_degree[i] == 0) 
        {
            q.push(i);
        }
    }

    std::vector<int> result; // 存储拓扑排序结果

    // 3. 处理队列中的顶点
    while (!q.empty()) 
    {
        int u = q.front();
        q.pop();
        result.push_back(u);

        // 遍历 u 的所有邻接点，并将其入度减 1
        for (int v : adj[u]) 
        {
            in_degree[v]--;
            // 如果邻接点 v 的入度变为 0，则将其入队
            if (in_degree[v] == 0) 
            {
                q.push(v);
            }
        }
    }

    // 4. 检查结果
    // 如果结果序列中的顶点数不等于总顶点数，说明图中存在环
    if (result.size() != n) 
    {
        return {}; // 返回空向量表示失败
    }

    return result;
}

int main() 
{
    int n = 6; //节点数
    std::vector<std::vector<int>> adj(n);

    // 添加依赖关系 (边)
    adj[0].push_back(1); 
    adj[0].push_back(2); 
    adj[1].push_back(2); 
    adj[2].push_back(5); 
    adj[2].push_back(3);
    adj[3].push_back(4);
    adj[4].push_back(5);

    std::cout << "--- Kahn 算法 ---" << std::endl;
    std::vector<int> sorted_order = topologicalSort_Kahn(n, adj);

    if (sorted_order.empty()) 
    {
        std::cout << "图中存在环，无法进行拓扑排序。" << std::endl;
    } 
    else 
    {
        std::cout << "一个可行的拓扑排序是: " << std::endl;
        for (int i = 0; i < sorted_order.size(); ++i) 
        {
            std::cout << sorted_order[i] << (i == sorted_order.size() - 1 ? "" : " -> ");
        }
        std::cout << std::endl;
    }

    return 0;
}

cpp

输出结果为：

--- Kahn 算法 ---
一个可行的拓扑排序是: 
0 -> 1 -> 2 -> 3 -> 4 -> 5

plaintext

排序的动画如下：

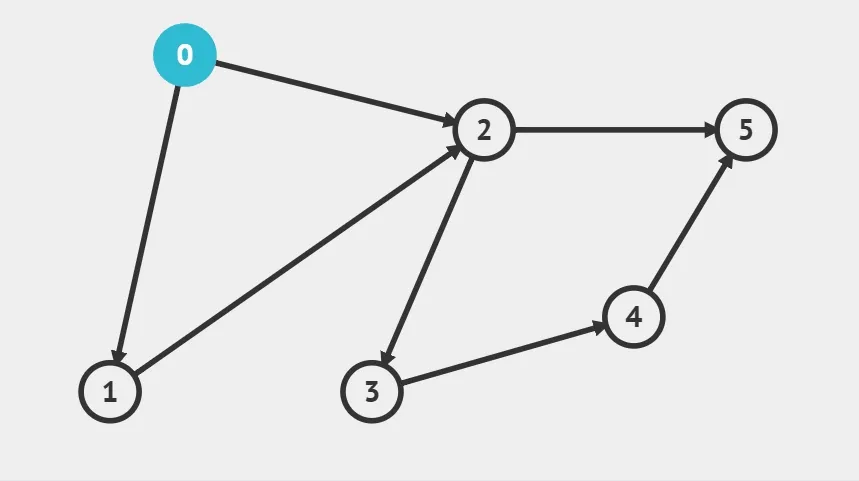
alt text

2.2 DFS 算法#

基于 DFS 的算法主要利用了 DFS 遍历图的特性。其核心思想是，一个顶点只有在它的所有后续顶点（它能到达的所有顶点）都被访问过之后，才算真正 “完成” 访问。算法步骤如下：

创建一个栈 (Stack) 来存储拓扑排序的结果。
创建一个集合 (Set) 或布尔数组 visited 来记录已访问过的顶点。
遍历图中的每一个顶点 u：
- 如果 u 没有被访问过，则以 u 为起点进行深度优先搜索。
深度优先搜索 (DFS) 函数 dfs(u) 的逻辑：
- 将当前顶点 u 标记为已访问。
- 遍历 u 的所有邻接顶点 v。
- 如果 v 没有被访问过，则递归调用 dfs(v)。
- 当从 u 出发的所有路径都探索完毕后（即所有邻接点都已被访问），将顶点 u 压入栈中。
最终结果：
- 当所有顶点都已被访问后，依次从栈中弹出所有元素，得到的序列就是拓扑排序的结果（逆序）。

如果想要在 DFS 中检测环，需要维护三种状态：

UNVISITED: 未访问
VISITING: 正在访问（当前递归栈中）
VISITED: 已访问完成

如果在 DFS 过程中，遇到了一个状态为 VISITING 的顶点，就说明图中存在环。

DFS 算法的 C++ 实现如下：

#include <iostream>
#include <vector>
#include <stack>
#include <string>
#include <algorithm>

// 顶点的访问状态
enum State { UNVISITED, VISITING, VISITED };

// DFS 辅助函数，发现环返回true，未发现则返回false
bool dfs(int u, const std::vector<std::vector<int>>& adj, std::vector<State>& visited, std::stack<int>& s) 
{
    visited[u] = VISITING; // 标记为正在访问

    for (int v : adj[u]) 
    {
        if (visited[v] == UNVISITED) 
        {
            if (dfs(v, adj, visited, s)) 
            {
                return true; // 如果在子调用中发现了环，立即返回
            }
        } 
        else if (visited[v] == VISITING) 
        {
            // 如果访问到一个正在访问的节点，说明存在环
            return true; 
        }
    }

    visited[u] = VISITED; // 节点 u 的所有邻接点都已访问完毕
    s.push(u); // 将 u 压入栈中
    return false; // 未发现环
}

// 基于 DFS 的拓扑排序实现
std::vector<int> topologicalSort_DFS(int n, const std::vector<std::vector<int>>& adj) 
{
    std::stack<int> s;
    std::vector<State> visited(n, UNVISITED);
    
    // 遍历所有顶点，以处理不连通的图
    for (int i = 0; i < n; ++i) 
    {
        if (visited[i] == UNVISITED) 
        {
            if (dfs(i, adj, visited, s)) 
            {
                // 如果 dfs 函数返回 true，说明检测到了环
                return {}; // 返回空向量表示失败
            }
        }
    }

    // 从栈中弹出元素，构造拓扑序列
    std::vector<int> result;
    while (!s.empty()) 
    {
        result.push_back(s.top());
        s.pop();
    }
    
    return result;
}


int main() {
    int n = 6; // 6 个节点
    std::vector<std::vector<int>> adj(n);

    // 添加依赖关系 (边)
    adj[0].push_back(1); 
    adj[0].push_back(2); 
    adj[1].push_back(2); 
    adj[2].push_back(3); 
    adj[2].push_back(5);
    adj[3].push_back(4);
    adj[4].push_back(5);

    std::cout << "--- DFS 算法 ---" << std::endl;
    std::vector<int> sorted_order = topologicalSort_DFS(n, adj);

    if (sorted_order.empty()) 
    {
        std::cout << "图中存在环，无法进行拓扑排序。" << std::endl;
    } 
    else 
    {
        std::cout << "一个可行的拓扑排序是: " << std::endl;
        for (int i = 0; i < sorted_order.size(); ++i) 
        {
            std::cout << sorted_order[i] << (i == sorted_order.size() - 1 ? "" : " -> ");
        }
        std::cout << std::endl;
    }

    return 0;
}

cpp

输出结果为：

--- DFS 算法 ---
一个可行的拓扑排序是: 
0 -> 1 -> 2 -> 3 -> 4 -> 5

plaintext

排序的动画如下：

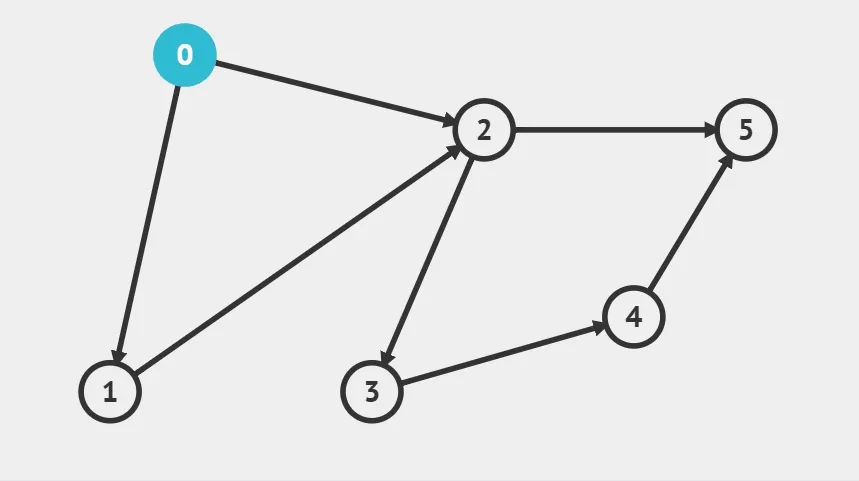
alt text

3. 复杂度分析#

时间复杂度：两种算法都需要遍历所有的顶点和所有的边一次，时间复杂度为 O(V+E)。

空间复杂度：Kahn 算法需要一个队列和数组来存储入度，DFS 算法需要递归栈空间和使用 visited 数组来记录数组的访问状态，空间复杂度都为 O(V)。