liangbm3's blog

Back
21 min read

堆及其相关应用

本文主要介绍堆这种数据结构，以及堆的相关应用，包括使用堆进行排序和使用堆来实现优先队列。
views | comments

1. 堆简介#

堆本质上是一棵树结构，其每个节点的键值都大于等于或者小于等于其父节点的键值。这里主要讨论的是二叉堆。

二叉堆是一种特殊的完全二叉树。完全二叉树是指，除了最后一层外，其他各层的节点数都达到最大，并且最后一层的节点都连续集中在左侧。除了结构上的要求，堆中的节点还需要满足堆序性：

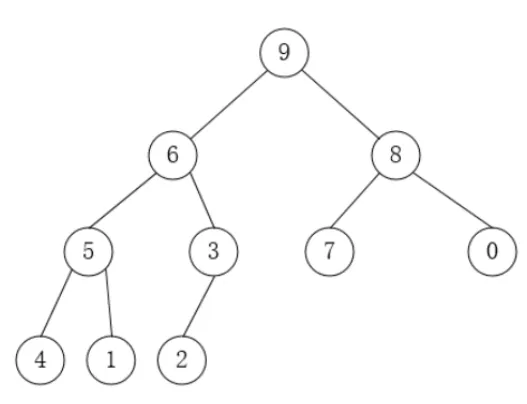
  • 最大堆（Max Heap）：每个节点的值都大于或等于其子节点的值。因此，堆顶（根节点）的元素是整个堆中的最大值。
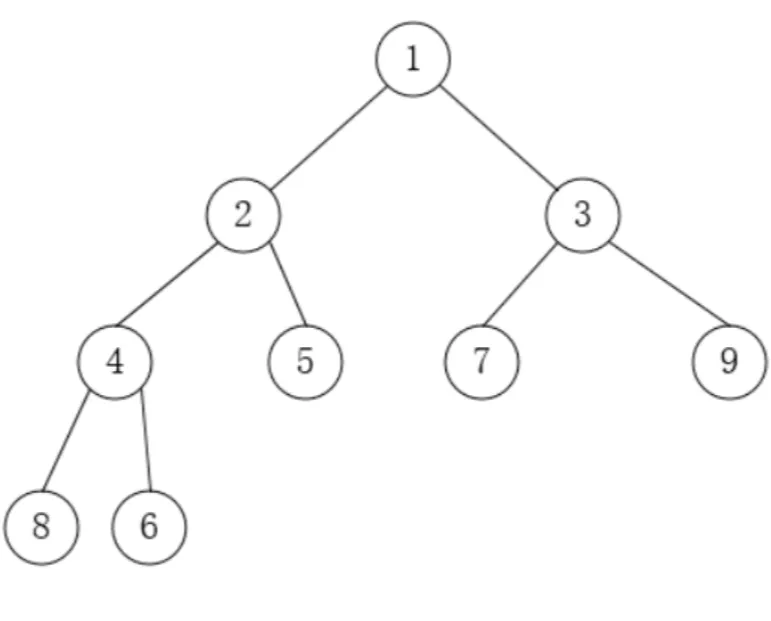
  • 最小堆（Min Heap）：每个节点的值都小于或等于其子节点的值。因此，堆顶（根节点）的元素是整个堆中的最小值。

最大堆：

最小堆：

2. 堆的存储#

尽管堆是树形结构，但它通常用数组来实现高效存储，堆节点在数组中的存储顺序通常是层序遍历的顺序，因此堆中的树节点和它的子节点在数组的索引是有数学关系的。对于数组中索引为 i 的节点：

  • 其父节点的索引为 floor((i-1)/2)
  • 其左子节点的索引为 2*i + 1
  • 其右子节点的索引为 2*i + 2

3. 堆的操作#

堆的操作主要有两种：插入和删除。插入和删除后都有可能不再满足堆的定义，需要重新进行调整，使其重新满足堆的特性，这个过程叫做堆化。堆化分为两种：上浮和下沉。

3.1 插入上浮#

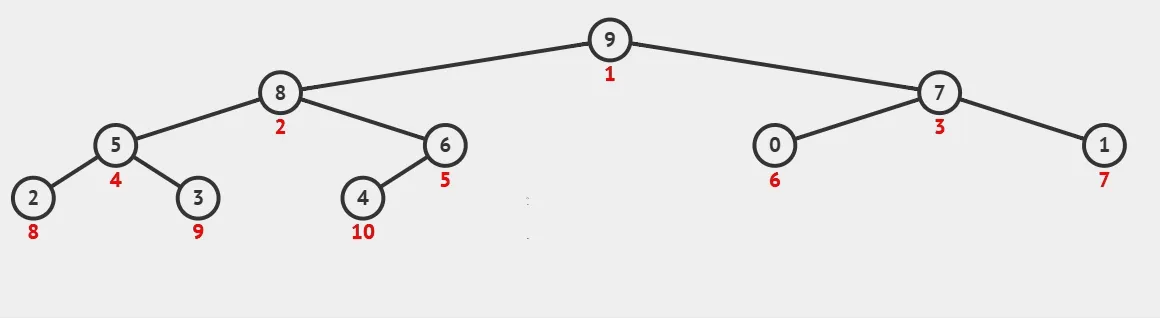
上浮主要用于插入操作中，执行插入时通常会把一个新元素添加到堆的末尾，这是它可能会比它的父节点更大（在最大堆中）或更小（在最小堆中），从而违反了堆属性。上浮操作就是将这个新元素与其父节点比较并交换，直到它找到合适的位置，恢复堆属性。以最大堆为例，插入的过程如下：

  1. 将新元素放在数组的末尾
  2. 比较新元素和它的父节点
  3. 如果新元素比父节点大，则交换它们
  4. 重复步骤 2 和 3，直到新元素不再比它的父节点大，或者它已经到达了堆顶

上浮操作的 C++ 实现如下：

void siftUp(vector<int>& heap, int idx)
{
    while (idx > 0)
    {
        int parent = (idx - 1) / 2;
        if (heap[idx] <= heap[parent]) break;  // 最大堆：子 ≤ 父，则停止
        swap(heap[idx], heap[parent]);
        idx = parent;
    }
}
cpp

插入操作的 C++ 实现如下：

void insert(vector<int>& heap, int value)
{
    heap.push_back(value);
    siftUp(heap, heap.size() - 1);
}
cpp

插入操作的动画：

alt text

3.2 删除下沉#

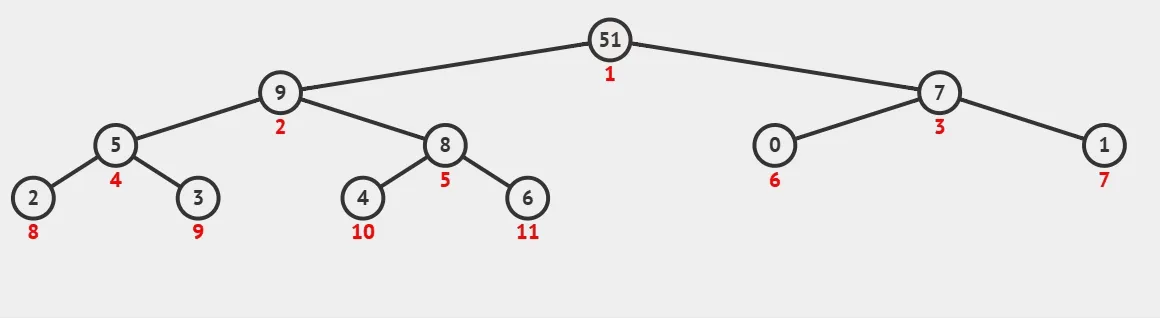
下沉主要用于删除操作中，执行删除操作将某个节点元素移除后，通常会用堆的最后一个元素来填补空缺。填补元素后很可能违反堆属性。下沉操作就是将这个元素与其子节点中较大者（在最大堆中）或较小者（在最小堆中）比较并交换，直到它找到合适的位置。以最大堆为例，删除的过程如下：

  1. 将堆的最后一个元素移动到删除位置
  2. 比较当前节点和它的左右子节点，找出最大的那个子节点
  3. 如果当前节点比它最大的子节点要小，则交换它们
  4. 重复步骤 2 和 3，顺着交换路径继续向下比较和交换，直到当前节点不再比它的任何子节点小，或者它已经成为一个叶子节点。

下沉操作的 C++ 实现如下：

void siftDown(vector<int>& heap, int idx)
{
    int n = heap.size();
    while (true)
    {
        int left = 2 * idx + 1;
        int right = 2 * idx + 2;
        int largest = idx;
        if (left < n && heap[left] > heap[largest]) largest = left;
        if (right < n && heap[right] > heap[largest]) largest = right;
        if (largest == idx) break;
        swap(heap[idx], heap[largest]);
        idx = largest;
    }
}
cpp

弹出（删除）堆顶点的 C++ 实现如下：

int popHeap(vector<int>& heap)
{
    if (heap.empty()) throw out_of_range("Heap is empty");
    int top = heap[0];
    heap[0] = heap.back();
    heap.pop_back();
    if (!heap.empty()) siftDown(heap, 0);
    return top;
}
cpp

弹出堆顶元素的动画：

alt text

4. 堆的构建#

从一个无序的元素集合构建一个完整堆的过程，通常被称为建堆，构建堆通常有两种方法：

  • 逐个插入法
  • 原地建堆法

4.1 逐个插入法#

逐个插入法的思路非常直观，首先初始化一个空的堆，然后遍历数组，将每个元素依次插入进堆里面，遍历完数组后即建堆完成。每次插入操作的时间复杂度是 O(log k)，其中 k 是堆中当前的元素数量。当插入 N 个元素时，总的时间复杂度为所有插入操作的总和，即 O(log 1) + O(log 2) + … + O(log N)，这最终可以近似为 O(N log N)。

C++ 实现如下：

void buildHeap(vector<int>& heap)
{
    vector<int> new_heap(heap.size());
    for(int val:heap)
    {
        insert(new_heap, val);
    }
    heap = new_heap;
}
cpp

构建的动画如下：

alt text

4.2 原地建堆法#

原地建堆法则是构建堆的标准算法，也叫 Floyd 算法，它比逐个插入法更加高效，它是一个自底向上的方法。构建的核心思想是将每一个叶子节点视为一个堆，因此只需要处理所有的非叶子节点，确保它们满足堆的属性即可。我们需要从最后一个非叶子节点开始，向前遍历直到根节点，对每个节点执行下沉操作。

算法的具体过程如下：

  • 将所有元素直接放入一个数组中，此时它只是一个完全二叉树，不一定是堆。
  • 找到最后一个非叶子节点的索引。对于一个大小为 N 的数组，该索引是 floor(N / 2) - 1。
  • 从这个索引开始，向前遍历到根节点（索引 0）。
  • 对遍历到的每个节点，执行下沉（siftDown）操作。

时间复杂度分析：虽然这个算法看起来像是执行了 N/2 次 siftDown 操作（每次 O(log N)），因此总的时间复杂度为 O(N log N)，但是这个直觉是错误的。更精确的数学分析表明，大部分节点的下沉路径都很短。越靠近底部的节点越多，但它们下沉的距离也越短。总的操作数可以被证明是一个与 N 呈线性关系的级数，因此时间复杂度为 O(N)。

C++ 实现如下：

void buildHeap(vector<int>& heap)
{
    int n = heap.size();
    // 最后一个非叶节点索引 = (n/2) - 1
    for (int i = n / 2 - 1; i >= 0; --i)
    {
        siftDown(heap, i);
    }
}
cpp

构建动画如下：

alt text

5. 堆排序#

堆排序是借助堆结构所实现的排序算法，通常使用大顶堆来实现升序排序，小顶堆来实现降序排序。核心思想是将数组转化为大顶堆（小顶堆）后，重复从大顶堆（小顶堆）中取出数值最大（数值最小）的节点，并让剩余的堆结构继续维持大顶堆（小顶堆）的性质。以大顶堆为例，堆排序算法的步骤如下：

  • 构建大顶堆：从最后一个非叶子节点开始，向前逐个对节点进行“下沉”调整，确保以该节点为根的子树满足最大堆的性质。经过一系列调整后，整个数组就变成了一个最大堆。
  • 执行排序：循环地将堆顶元素（当前最大值）与堆末尾的元素交换，然后缩小堆的范围并重新调整堆，使其继续满足最大堆的性质。
  • 当所有元素都从堆中移除后，数组就变成了一个有序的升序序列。

时间复杂度：堆排序的时间复杂度为 O(nlogn)。其中，建堆的过程需要 O(n) 的时间，而之后每次调整堆需要 O(logn) 的时间，共进行 n-1 次。

空间复杂度：堆排序是一种原地排序算法，它只需要一个常数级别的额外空间来存储临时变量，因此空间复杂度为 O(1)。

C++ 实现如下：

class maxHeap
{
private:
    vector<int> heap;
    void siftdown(int idx,int n)
    {
        while(true)
        {
            int left=2*idx+1;
            int right=2*idx+2;
            int largest=idx;
            if(left<n && heap[left]>heap[largest]) largest=left;
            if(right<n && heap[right]>heap[largest]) largest=right;
            if(largest==idx) break;
            swap(heap[idx],heap[largest]);
            idx=largest;
        }
    }
public:
    void buildMaxHeap(const vector<int>& arr)
    {
        heap=arr;
        int n=heap.size();
        for(int i=(n-2)/2;i>=0;i--)
        {
            siftdown(i,n);
        }
    }
    //堆排序
    vector<int> maxHeapSort(const vector<int>& nums)
    {
        //建堆
        buildMaxHeap(nums);
        int n=heap.size();
        //从最后一个元素开始
        for(int i=n-1;i>0;i--)
        {
            //将堆顶元素放在尾部
            swap(heap[0],heap[i]);
            //缩小堆结构的范围并进行下沉
            siftdown(0,i);
        }
        return heap;
    }
};

class Solution
{
public:
    vector<int> sort(vector<int> nums)
    {
        return maxHeap().maxHeapSort(nums);
    }
};
cpp

6. 优先队列#

6.1 简介#

优先队列是一种特殊的队列，优先队列的元素都会被赋予一个优先级，元素的出队顺序由优先级决定：高优先级的元素先于低优先级的元素出队。如果多个元素具有相同的优先级，则它们的相对顺序没有明确规定。

6.2 应用场景#

优先队列具有广泛的应用场景，包括：

  • 操作系统任务调度: 操作系统需要管理多个同时运行的进程。优先队列被用来调度 CPU 时间，高优先级的进程（如系统进程）会比低优先级的用户进程先获得执行权。
  • 图算法:
    • Dijkstra 最短路径算法: 在寻找图中从一个顶点到所有其他顶点的最短路径时，Dijkstra 算法使用一个最小优先队列来存储待访问的顶点。队列根据已知的从源点到该顶点的距离进行排序，每次从未访问的顶点中选择距离最短的一个进行处理。
    • Prim 最小生成树算法: Prim 算法使用最小优先队列来选择连接到当前生成树的、权重最小的边，从而逐步构建最小生成树。
  • 事件驱动模拟 (Event-Driven Simulation): 在模拟系统中，事件被存储在一个以时间为优先级的最小优先队列中。模拟器总是从队列中取出时间最早的事件进行处理，处理该事件可能会触发新的未来事件加入队列。
  • 数据压缩 (Huffman Coding): 在构建霍夫曼树时，使用一个最小优先队列来存储字符及其频率。算法重复地从队列中取出两个频率最低的节点，合并它们，然后将新生成的父节点放回队列，直到队列中只剩一个节点（即霍夫曼树的根）。
  • A* 搜索算法: 这是广泛用于寻路和图遍历的算法。它使用一个优先队列来决定下一步要探索的节点，其优先级由“已付出的代价”（g-score）和“到目标的预估代价”（h-score）共同决定。

6.3 实现#

优先队列的实现方法有很多种：基于数组或链表的实现方式如下：

  • 无序数组或链表： 插入操作非常简单，只需将新元素添加到数组末尾或链表头部即可，时间复杂度为 O(1)。但要查找并删除最高优先级的元素，则需要遍历整个数据结构，找到目标元素，这需要 O(n) 的时间。
  • 有序数组或链表： 如果我们维持一个按优先级排序的数组或链表，那么查看和删除最高优先级的元素（位于数组或链表的一端）将非常快，仅需 O(1)。然而，为了在插入新元素时保持有序性，可能需要移动大量元素，导致插入操作的时间复杂度为 O(n)。

更加常用的且高效是基于二叉堆的实现方式：

  • 插入: 将新元素添加到堆的末尾，然后通过与其父节点比较和交换，一路“上浮”到正确的位置以维持堆属性。这个过程最多移动树的高度，即 O(logn)。
  • 删除: 将根节点（最高优先级元素）与最后一个元素交换，然后移除根节点。接着，新的根节点通过与子节点比较和交换，一路“下沉”到正确的位置以恢复堆属性。这个过程的时间复杂度也是 O(logn)。

6.4 C++ 中的优先队列#

在 C++ 中，<priority_queue> 是标准模板库（STL）的一个容器适配器，，用于实现优先队列。默认情况下，队列中最大的元素拥有最高的优先级。

std::priority_queue 是一个模板类，其声明格式如下：

template <
    class T, // 元素类型
    class Container = std::vector<T>, // 底层容器类型，必须支持随机访问迭代器
    class Compare = std::less<T> // 比较函数对象，决定优先级
> class priority_queue;
cpp

常用操作：

  • empty(): 检查队列是否为空。
  • size(): 返回队列中的元素数量。
  • top(): 返回队列顶部的元素（不删除它）。
  • push(): 向队列添加一个元素。
  • pop(): 移除队列顶部的元素。

C++ 的 priority_queue 默认使用 std::less<T> 比较器，队列中最大的元素具有最高优先级，如果要最小的元素具有最低优先级，可以传入std::greater<T>比较器。例如：

std::priority_queue<int, std::vector<int>, std::greater<int>> min_heap;
cpp

如果是在优先队列中存储自定义的结构体或类时，则需要告诉 std::priority_queue 如何比较它们。有以下几种常用方法：

  • 重载 < 运算符。这种方法比较直接，例如： 
    struct Task 
{
    int priority;
    std::string name;

    // 重载 < 运算符，priority 值越大，优先级越高
    bool operator<(const Task& other) const {
        return this->priority < other.priority;
    }
};
    cpp
  • 提供自定义比较函数对象。这种方法更加灵活，可以不修改类本身，例如： 
    struct Task 
{
    int priority;
    std::string name;
};

// 自定义比较函数对象
struct CompareTask 
{
    // 返回 true 表示 a 的优先级比 b 低
    bool operator()(const Task& a, const Task& b) 
    {
        return a.priority < b.priority; // 最大堆
        // return a.priority > b.priority; // 若要最小堆，则反向比较
    }
};
    cpp
  • 使用 Lambda 表达式。对于局部的、一次性的比较逻辑，使用 Lambda 表达式非常方便。例如： 
    struct Point 
{
    int x, y;
    int dist_from_origin() const { return x*x + y*y; }
};

auto compare_points = [](const Point& a, const Point& b) {
    // 距离原点越近，优先级越高 (最小堆)
    return a.dist_from_origin() > b.dist_from_origin();
};
    cpp
堆及其相关应用
https://liangbm3.site/blog/dui-ji-qi-xiang-guan-ying-yong
Author liangbm3
Published at 2025年7月7日
Copyright CC BY-NC-SA 4.0

并查集

拓扑排序
Comment seems to stuck. Try to refresh?✨