最小生成树

1. 简介#

最小生成树（Minimum Spanning Tree，简称 MST） 是图论中的一个重要概念，主要应用于带权无向连通图中。给定一个带权无向连通图，它的最小生成树包含图中所有的顶点，但只包含一部分边，并且满足以下三个条件：

是一棵树：这意味着图中没有任何环路
是一棵生成树：这意味着包含图中的所有顶点
权重之和最小：在所有可能的生成树中，它的所有边的权重之和是最小的

例如对于下面的带权无向连通图：

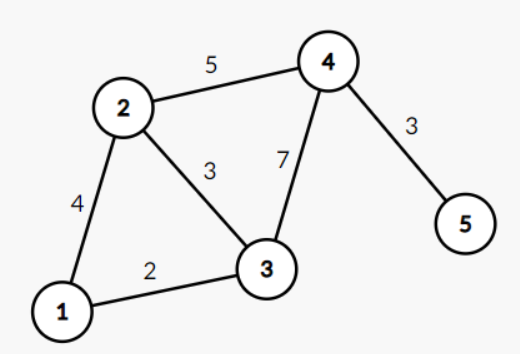
它的最小生成树为：

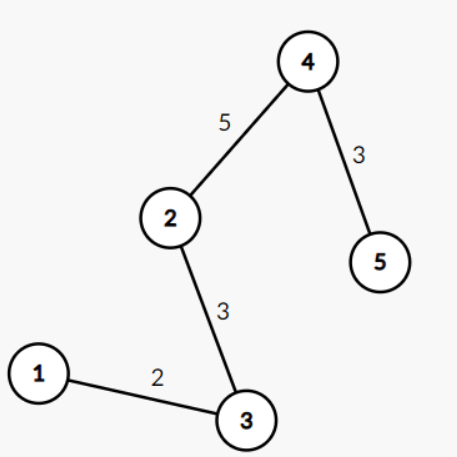
最小生成树有两个非常重要的性质，是构建算法的基础：

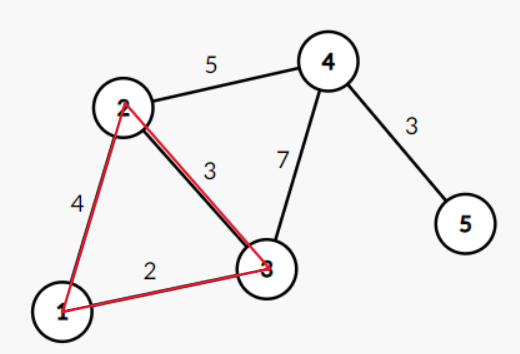
切割性质（Cut Property）：将图中的所有顶点分成两个不相交的集合。在所有横跨这两个集合的边中（即一个端点在一个集合，另一个端点在另一个集合），权重最小的那条边，必定属于图的某一个最小生成树。例如按蓝色这条线切割，权重为5这条边肯定属于最小生成树：
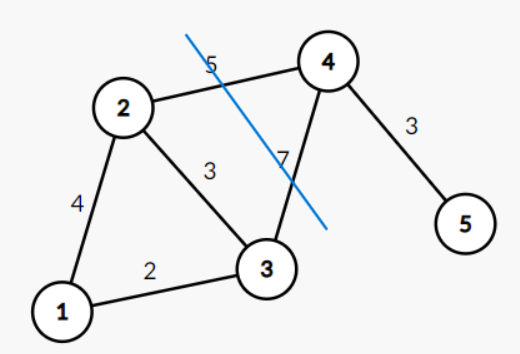
环路性质（Cycle Property）：对于图中的任意一个环路。这个环路中权重最大的那条边，一定不属于任何一个最小生成树。例如对于红色这个环路，权重为4这条边肯定不属于最小生成树：

2. 应用场景#

最小生成树在日常有着广泛的应用，主要用于解决如何以最低成本连接所有点的问题：

网络设计：铺设通信电缆、输水管道、电网、公路网等，目标是覆盖所有地点且总长度或成本最低。
聚类分析：在数据科学中，可以用来帮助识别数据点簇。
电路设计：在设计电路板时，确保所有引脚都连接起来，并且使用的导线总长度最短。
近似算法：在解决一些更复杂的问题（如旅行商问题）时，最小生成树可以作为一个很好的近似解或解决过程中的一个步骤。

3. 经典算法#

寻找最小生成树主要有三种经典算法，分别是：Prim 算法、Kruskal 算法和 Boruvka 算法。其中 Boruvka 的并行友好特性使其在高性能计算和处理大规模图数据时具有不可替代的优势。我们这里主要讨论的是Prim 算法和Kruskal 算法，它们两个都是属于贪心算法，即在每一步都做出当前的最优选择，最终得到全局最优解。

3.1 Kruskal 算法#

Kruskal 算法（克鲁斯卡尔算法） 的思路是：从权重最小的边开始，依次考察所有边。如果当前这条边连接的两个顶点还没有被连通（即加入这条边不会形成环路），就将它加入到最小生成树中。重复这个过程，直到加入了 n-1 条边为止（对于一个有 n 个顶点的图，其生成树恰好有 n-1 条边）。具体步骤：

将图中所有的边按照权重从小到大进行排序，然后创建一个只包含所有顶点但没有边的图，每个顶点初始时都各自属于一个独立的集合。
从排序好的边中，依次取出权重最小的边。
判断这条边的两个顶点是否属于同一个集合（如果属于，说明它们已经连通，加入这条边会形成环路）。属于则跳过，不属于则加入到最小生成树中
重复步骤4，直到最小生成树中有 n-1 条边。

Kruskal 算法的 C++ 实现如下：

#include <iostream>
#include <vector>
#include <algorithm>
#include <numeric>

// 定义边的结构体
struct Edge
{
    int src, dest, weight;
};

// 并查集结构体
struct UnionFind
{
    std::vector<int> parent;
    UnionFind(int n)
    {
        parent.resize(n);
        // 初始化，每个元素的父节点都是它自己
        for (int i = 0; i < n; ++i)
        {
            parent[i] = i;
        }
    }

    // 查找元素i所在集合的根节点（带路径压缩）
    int Find(int i)
    {
        if (parent[i] == i)
            return i;
        return parent[i] = Find(parent[i]);
    }

    // 合并i和j所在的集合
    void Union(int i, int j)
    {
        int root_i = Find(i);
        int root_j = Find(j);
        if (root_i != root_j)
        {
            parent[root_i] = root_j;
        }
    }
};

// 比较函数，用于排序
bool compareEdges(const Edge &a, const Edge &b)
{
    return a.weight < b.weight;
}

// Kruskal算法主函数
void kruskalMST(int V, std::vector<Edge> &edges)
{
    // 1. 按权重对所有边进行升序排序
    std::sort(edges.begin(), edges.end(), compareEdges);

    UnionFind union_find(V);
    std::vector<Edge> resultMST;
    int totalWeight = 0;

    // 2. 遍历排序后的边
    for (const auto &edge : edges)
    {
        int u = edge.src;
        int v = edge.dest;

        // 3. 如果加入这条边不会形成环路
        if (union_find.Find(u) != union_find.Find(v))
        {
            // 将这条边加入结果集
            resultMST.push_back(edge);
            totalWeight += edge.weight;

            // 合并两个顶点的集合
            union_find.Union(u, v);
        }

        // 当MST中的边数达到 V-1 时，可以提前结束
        if (resultMST.size() == V - 1)
            break;
    }

    // 打印结果
    std::cout << "Kruskal 算法找到的最小生成树如下:" << std::endl;
    for (const auto &edge : resultMST)
    {
        std::cout << "边 " << edge.src << " - " << edge.dest << "   权重: " << edge.weight << std::endl;
    }
    std::cout << "最小生成树的总权重: " << totalWeight << std::endl;
}

int main()
{
    int V = 5; // 顶点数
    std::vector<Edge> edges =
        {
            {0, 1, 2},
            {0, 3, 6},
            {1, 2, 3},
            {1, 3, 8},
            {1, 4, 5},
            {2, 4, 7},
            {3, 4, 9}
        };

    kruskalMST(V, edges);

    return 0;
}

cpp

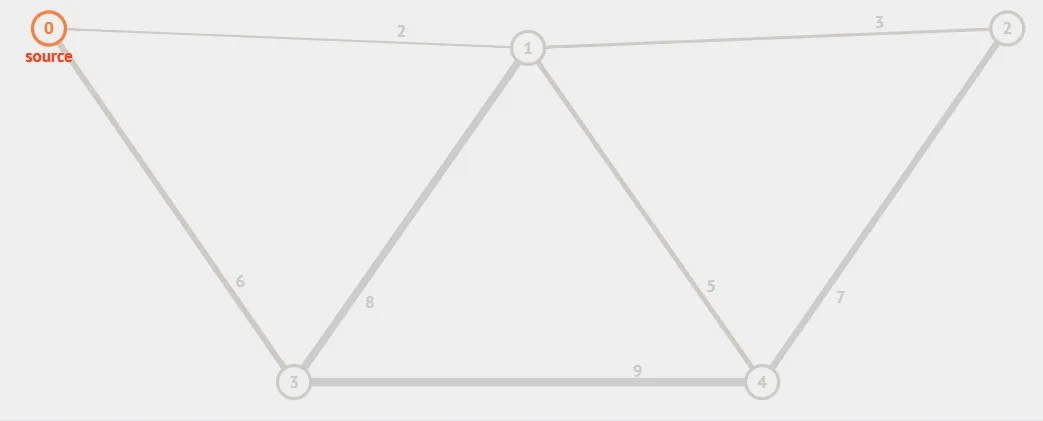
算法输出：

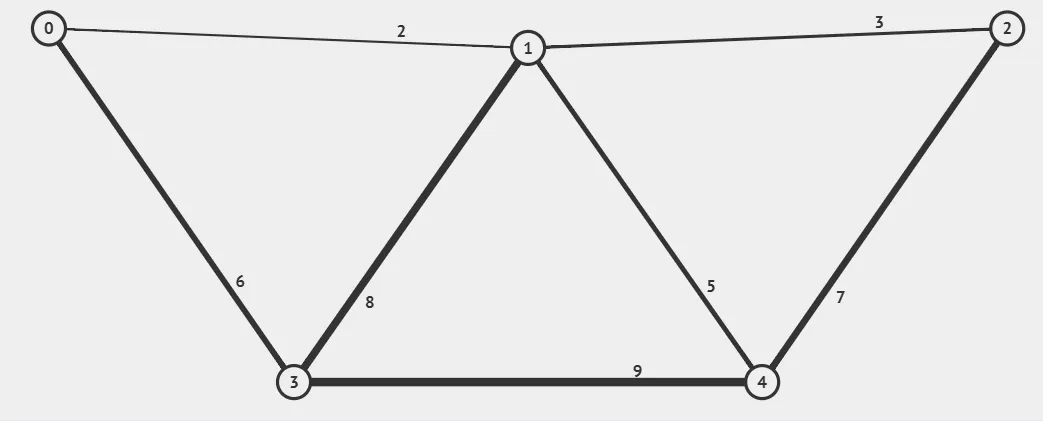
Kruskal 算法找到的最小生成树如下:
边 0 - 1   权重: 2
边 1 - 2   权重: 3
边 1 - 4   权重: 5
边 0 - 3   权重: 6
最小生成树的总权重: 16

plaintext

动画演示：

alt text

3.2 Prim 算法#

Prim 算法（普里姆算法） 的思路是：从任意一个顶点开始，逐步扩大一棵正在生长的树。在每一步，都寻找一条连接树内顶点和树外顶点的、权重最小的边，并将这条边和它所连接的树外顶点加入到树中。重复这个过程，直到所有顶点都被加入。具体步骤：

选择任意一个顶点作为起始点，将其加入到一个集合 U 中（表示已经是最小生成树的一部分）。
寻找所有一个端点在集合 U 中，另一个端点不在 U 中的边。在这些边中，找到权重最小的那一条。
将这条权重最小的边和它连接的那个不在 U 中的顶点加入到最小生成树和集合 U 中。
重复步骤2-3，直到所有顶点都加入了集合 U

Prim 算法的 C++ 实现如下：

#include <iostream>
#include <vector>
#include <queue>
#include <limits>

// 定义一个类型别名，方便使用
// pair<权重, 顶点>
using iPair = std::pair<int, int>;

// Prim算法主函数
void primMST(int V, const std::vector<std::vector<iPair>> &adj)
{
    // 使用优先队列作为最小堆，存储 {权重, 顶点}
    // std::greater 使其成为最小堆
    // 优先队列会使用pair的第一个元素（权重）进行排序，如果第一个元素相同再排序第二个元素（顶点）
    std::priority_queue<iPair, std::vector<iPair>, std::greater<iPair>> pq;

    // 选择顶点0作为起始点
    int src = 0;

    // 存储连接到MST的最小权重，初始化为无穷大
    // 如果为无穷大，表示这个权重对应的边的两个顶点都没有在最小生成树中
    std::vector<int> minWeight(V, std::numeric_limits<int>::max());
    // 存储父节点，用于构建最小生成树（MST），便于打印输出结果
    std::vector<int> parent(V, -1);
    // 标记顶点是否访问过
    std::vector<bool> visited(V, false);

    // 初始化起始点
    pq.push({0, src});
    minWeight[src] = 0;

    int totalWeight = 0;

    while (!pq.empty())
    {
        // 从优先队列中取出权重最小的顶点
        int u = pq.top().second;
        // 取出顶点的权重
        int w = pq.top().first;
        pq.pop();

        // 如果顶点已经处理过，则跳过，防止环路
        if (visited[u])
        {
            continue;
        }

        // 将顶点标记为已访问
        visited[u] = true;
        totalWeight += w;

        // 遍历u的所有邻接点
        for (const auto &edge : adj[u])
        {
            int weight = edge.first;
            int v = edge.second;

            // 如果v没有访问过，并且通过u连接v的权重更小
            if (!visited[v] && minWeight[v] > weight)
            {
                // 更新v的minWeight值和父节点
                minWeight[v] = weight;
                pq.push({weight, v});
                parent[v] = u;
            }
        }
    }

    // 打印结果
    std::cout << "Prim 算法找到的最小生成树如下:" << std::endl;
    for (int i = 1; i < V; ++i)
    {
        // minWeight[i] 就是连接 parent[i] 和 i 的边的权重
        std::cout << "边 " << parent[i] << " - " << i << "   权重: " << minWeight[i] << std::endl;
    }
    std::cout << "最小生成树的总权重: " << totalWeight << std::endl;
}

int main()
{
    int V = 5;
    // 使用邻接表表示图
    std::vector<std::vector<iPair>> adj(V);

    //使用lambda表达式构建邻接表
    auto addEdge = [&](int u, int v, int w)
    {
        adj[u].push_back({w, v});
        adj[v].push_back({w, u});
    };

    addEdge(0, 1, 2);
    addEdge(0, 3, 6);
    addEdge(1, 2, 3);
    addEdge(1, 3, 8);
    addEdge(1, 4, 5);
    addEdge(2, 4, 7);
    addEdge(3, 4, 9);

    primMST(V, adj);

    return 0;
}

cpp

动画演示：

alt text